Navigation :

Development

Here is the DOXYGEN generated documentation.

This section is devoted to particularly difficult or tricky parts of the GPUE codebase that deserve special attention for future development. More information will come as features are developed.

CuFFT usage with angular momentum/gauge fields

To implement angular momentum in the split-operator based pseudo-spectral methods, we must take special care of these evolution operators. As outlined in O’Riordan, 2017, th non-commutative nature of the position and momentum space operators required for angular momentum present a challenge — we cannot truly implment a numerical model without a certain degree of error. This is well documented in the above literature, though what is not discussed is an implementation of this method using CUDA and the CuFFT library.

Let’s assume that we have a 3D dataset, with the data layout given by the following figure:


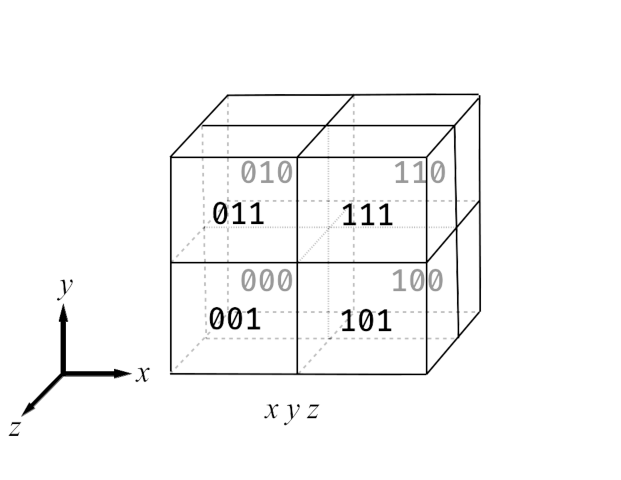
Fig. 1: Data layout for a $2\times 2\times 2$ grid.

For simplicity we assume a $2\times 2\times 2$ grid, giving us 8 data elements. Here we assume indexing is performed along $(x,y,z)$, where $x$ is the fastest axis and $z$ is the slowest axis.

For rotation about a specific axis, we assume that the applied operator is applied in a planar (2D) manner that is constant along this axis. In other words, $\Omega_z = x\p_y - yp_x$. For our split-operator method, we attain the $k$-space basis along a specific axis by performing a Fourier transform along this axis, and with appropriate scaling the resulting momentum space basis.

Let us now look at the layout of the data in memory for the above $2^3$ cube. In the given layout, keeping $y,z$ constant, all $x$ data elements are adjacent. This is optimal for computational performance, as CUDA loads data in the width of warps at any instance. Data loads are expensive, and to allow for the best performance we must keep loads (aka reads) to a minimum. To act along the $x$ axis, given that the data is always adjacent, Fourier transforms can be nicely batched to transform each respective $x$, for each combination of $y,z$.


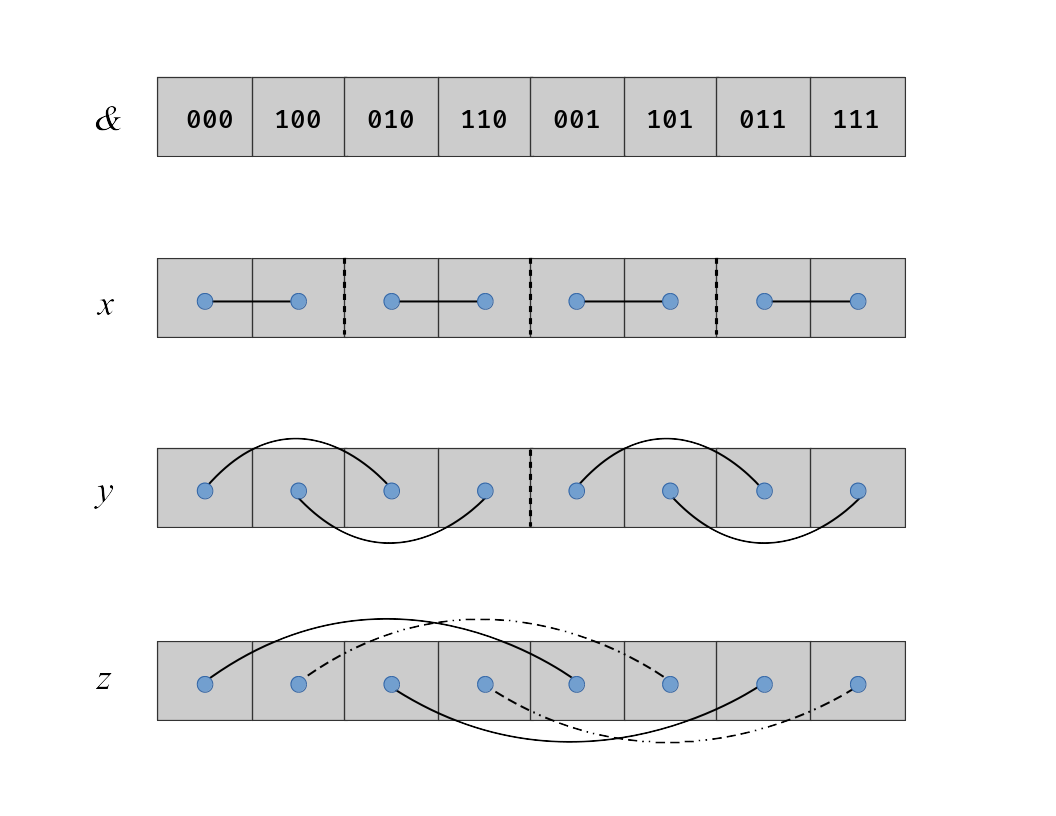
Fig. 2: Memory locations and connections for data along each respective axis. $x$-axis data is adjacent, and hence is the fastest to process as data is chunks of CUDA warp sizes. The dashed straight lines represent the individual divisions between indendent data for transforming. The curved lines show the links between data of the same (dependent) transforms.

If we wish to transform along one of the other axes, say $y$, this becomes a challenge, as the data layout is no longer adjacent. To calculate $\Omega_z$ we require the calculation of $p_x$ and $p_y$, thus we must deal with this non-adjacency for any rotation operations. The CuFFT API supports 1D, 2D, 3D, and n-D transforms, but only assumes transforms are performed over all dimensions of a dataset (ie, there are no functions for selective transformation of a single axis). One might say, that this is appropriately solved by a transpose in 2D, or a permutation in 3+ dimensions. As of the time of writing, no open-source in-place memory transpose/permutations exists, and out-of-place is not an option to enable storage of 3D data sets on the GPU. CuFFT has internal tranpose operations, but none that are publically exposed (these functions are called as part of the FFT transform calls, and observable in cuda-gdb or nvprof).

An initial implementation to calculate the appropriately transformed data using the in-built CuFFT functions can be performed by batching 1D FFT’s for the adjacent ($x$) data set, and 2D forward-1D invserse (2DF-1DI) for the non-adjacent ($y$) data. This transforms the data along a 2D slice, and inverses the adjacent data set, so the remaining data set is the Fourier transformed non-adjacent data. However, this method is extremely inefficient, as it performs many more transforms than necessary. We can instead manipulate the data by appropriately batched CuFFT tranforms, making use of the manual control provided by cufftPlanMany, wherein we can control the stride, distance, offsets and size of the data being transformed. While not as performant as an FFT over adjacent data, the prior constraint of no out-of-place transposes/permutes is maintained as we are strictly using CuFFT function calls, leaving the underlying implementation to manipulate the data transforms.

Param	Property
`inembed`	Number of elements in input data to be transformed
`onembed`	Number of elements in output data following transform
`idist`	Spacing between consecutive input data sets in memory for batched transforms
`odist`	Spacing between consecutive output data sets in memory following batched transforms
`istride`	Spacing between input data elements in the same dataset in memory
`ostride`	Spacing between output data elements in the same dataset in memory
`batch`	Number of transforms to perform in batched mode

The following script demonstrates the use of the above parameters to control the transforms in 2D and 3D. The transform of the fast-axis ($x$) data is simply performed by using batched 1D transforms using cufftPlan1d, with the comparative result obtained also from the cufftPlanMany method using the above parameters. To transform the non-adjacent ($y$) data, first we examine the 2DF-1DI result as previously mentioned, and compare the result with the cufftPlanMany method. In 2D this is natively supported by giving the above parameters the appropriate values for the data set. In 3+ dimensions it is worth noting that for this to work we must shift the pointer of the data by the product of the length of all faster axes dimensions. The slowest axis can simply be treated then without any need for pointer shifting. The earlier figure shows dotted lines wherever the transform boundaries do not cross.

#include <stdio.h>
#include <cstdlib>
#include <cufft.h>
#include <cuda.h>
#include <iostream>
#include <assert.h>

// ********************************************************* //
// Error checking macros
// ********************************************************* //

#define ERR_CHECK(err_val) {                                    \
    cudaError_t err = err_val;                                  \
    if (err != cudaSuccess) {                                   \
        fprintf(stderr, "Error %s at line %d in file %s\n",     \
                cudaGetErrorString(err), __LINE__, __FILE__);   \
        exit(1);                                                \
    }                                                           \
}

#define FFT_ERR_CHECK(err_val) {                                \
    cufftResult err = err_val;                                  \
    if (err != CUFFT_SUCCESS) {                                 \
        fprintf(stderr, "Error %d at line %d in file %s\n",     \
                err, __LINE__, __FILE__);                       \
        exit(1);                                                \
    }                                                           \
}

// ********************************************************* //
// FT params for ...many plans
// ********************************************************* //

typedef struct FTParams{
    int numTranforms;
    int numLoops;
    int stride;
    int dist;
    int offset;
};

// ********************************************************* //
// Sample cuda kernels
// ********************************************************* //

__host__ __device__ double retVal(double val) {
    return val;
}

__global__ void copyVal(double *inData, double *outData) {
    outData[threadIdx.x] = inData[threadIdx.x];
}

// ********************************************************* //
// FT test functions
// ********************************************************* //

void fftIt2D(){
    cudaDeviceReset();
    int dimSize = 6;
    int NX = dimSize*dimSize;

    int numTransform = std::round(sqrt(NX));
    int sqrtNX = std::round(sqrt(NX));
    int dims1D[] = {(NX)};
    int dims2D[] = {sqrtNX,sqrtNX};

    int rank = 1;

    int inembed[] = {NX}; 
    int onembed[] = {NX};
    int istride[] = {1,sqrtNX}; // Consecutive elements, same signal 
    int ostride[] = {1,sqrtNX}; //
    int idist[] = {sqrtNX,1}; // Consecutive signals
    int odist[] = {sqrtNX,1};

    cufftHandle planMany, plan1D, plan2D;
    cufftDoubleComplex *data_H1DFFT, *data_H2DF1DI, *data_HmanyFFT, *data_H0, *data_D;

    ERR_CHECK( cudaMalloc( (cufftDoubleComplex**) &data_D, sizeof(cufftDoubleComplex)*NX) );
    data_H1DFFT = (cufftDoubleComplex*) malloc(sizeof(cufftDoubleComplex)*NX);
    data_H2DF1DI = (cufftDoubleComplex*) malloc(sizeof(cufftDoubleComplex)*NX);
    data_HmanyFFT = (cufftDoubleComplex*) malloc(sizeof(cufftDoubleComplex)*NX);
    data_H0 = (cufftDoubleComplex*) malloc(sizeof(cufftDoubleComplex)*NX);

    // ********************************************************* //
    // Create the input data
    // ********************************************************* //
    std::cout << "INPUT:\n";
    for(int ii=0; ii<sqrtNX; ++ii){
        for(int jj=0; jj<sqrtNX; ++jj){
            data_H0[jj + ii*sqrtNX].x = (double) ii;
            data_H0[jj + ii*sqrtNX].y = (double) jj;
            std::cout << data_H0[jj + ii*sqrtNX].x << " + 1i*" << data_H0[jj + ii*sqrtNX].y << "\t";
        }
        std::cout << "\n";
    }
    std::cout << "\n";

    ERR_CHECK( cudaMemcpy(data_D, data_H0, sizeof(cufftDoubleComplex) * NX, cudaMemcpyHostToDevice));

    // ******************************************************************************** //
    // First, check the 1D FFT along the standard dimension
    // ******************************************************************************** //
    FFT_ERR_CHECK(cufftPlan1d(&plan1D, dims2D[0], CUFFT_Z2Z, numTransform));
    FFT_ERR_CHECK(cufftExecZ2Z(plan1D, data_D, data_D, CUFFT_FORWARD));
    ERR_CHECK(cudaMemcpy(data_H1DFFT, data_D, sizeof(cufftDoubleComplex) * NX, cudaMemcpyDeviceToHost));
    std::cout << "OUTPUT 1D:\n";
    for(int ii=0; ii<sqrtNX; ++ii){
        for(int jj=0; jj<sqrtNX; ++jj){
            std::cout << data_H1DFFT[jj + ii*sqrtNX].x << " + 1i*" << data_H1DFFT[jj + ii*sqrtNX].y << "\t";
        }
        std::cout << "\n";
    }

    //Overwrite GPU data to original values
    ERR_CHECK( cudaMemcpy(data_D, data_H0, sizeof(cufftDoubleComplex) * NX, cudaMemcpyHostToDevice));

    // ******************************************************************************** //
    // ******************************************************************************** //
    // Next, check the Many FFT along the same expected dimension
    // ******************************************************************************** //

    FFT_ERR_CHECK(cufftPlanMany(&planMany, rank, dims2D, inembed, istride[0], idist[0], onembed, ostride[0], odist[0], CUFFT_Z2Z, numTransform));
    FFT_ERR_CHECK(cufftExecZ2Z(planMany, data_D, data_D, CUFFT_FORWARD));

    ERR_CHECK(cudaMemcpy(data_HmanyFFT, data_D, sizeof(cufftDoubleComplex) * NX, cudaMemcpyDeviceToHost));

    std::cout << "OUTPUT MANY 1D:\n";
    for(int ii=0; ii<sqrtNX; ++ii){
        for(int jj=0; jj<sqrtNX; ++jj){
            std::cout << data_HmanyFFT[jj + ii*sqrtNX].x << " + 1i*" << data_HmanyFFT[jj + ii*sqrtNX].y << "\t";
        }
        std::cout << "\n";
    }

    try {
        for (int ii=0; ii<NX; ++ii){
            assert( (data_H1DFFT[ii].x - data_HmanyFFT[ii].x) < 1e-7  );
            assert( (data_H1DFFT[ii].y - data_HmanyFFT[ii].y) < 1e-7  );
        }
    } catch (const char* msg) {
        std::cerr << msg << std::endl;
    }
    //Overwrite GPU data to original values
    ERR_CHECK( cudaMemcpy(data_D, data_H0, sizeof(cufftDoubleComplex) * NX, cudaMemcpyHostToDevice));

    // ******************************************************************************** //
    // Check the 2D FFT Forward, 1D FFT back
    // ******************************************************************************** //
    FFT_ERR_CHECK(cufftPlan2d(&plan2D, dims2D[0], dims2D[1], CUFFT_Z2Z));
    FFT_ERR_CHECK(cufftExecZ2Z(plan2D, data_D, data_D, CUFFT_FORWARD));
    FFT_ERR_CHECK(cufftExecZ2Z(plan1D, data_D, data_D, CUFFT_INVERSE));

    ERR_CHECK(cudaMemcpy(data_H2DF1DI, data_D, sizeof(cufftDoubleComplex) * NX, cudaMemcpyDeviceToHost));
    std::cout << "OUTPUT 2DF-1DI:\n";
    for(int ii=0; ii<sqrtNX; ++ii){
        for(int jj=0; jj<sqrtNX; ++jj){
            std::cout << data_H2DF1DI[jj + ii*sqrtNX].x/sqrtNX << " + 1i*" << data_H2DF1DI[jj + ii*sqrtNX].y/sqrtNX << "\t";
        }
        std::cout << "\n";
    }
    //Overwrite GPU data to original values
    ERR_CHECK( cudaMemcpy(data_D, data_H0, sizeof(cufftDoubleComplex) * NX, cudaMemcpyHostToDevice));

    // ******************************************************************************** //
    // ******************************************************************************** //
    // Lastly, check the Many FFT along the other dimension
    // ******************************************************************************** //

    FFT_ERR_CHECK(cufftPlanMany(&planMany, rank, dims2D, inembed, istride[1], idist[1], onembed, ostride[1], odist[1], CUFFT_Z2Z, sqrtNX));
    FFT_ERR_CHECK(cufftExecZ2Z(planMany, data_D, data_D, CUFFT_FORWARD));

    //ERR_CHECK(cudaDeviceSynchronize());
    ERR_CHECK(cudaMemcpy(data_HmanyFFT, data_D, sizeof(cufftDoubleComplex) * NX, cudaMemcpyDeviceToHost));

    std::cout << "OUTPUT MANY 1D Other:\n";
    for(int ii=0; ii<sqrtNX; ++ii){
        for(int jj=0; jj<sqrtNX; ++jj){
            std::cout << data_HmanyFFT[jj + ii*sqrtNX].x << " + 1i*" << data_HmanyFFT[jj + ii*sqrtNX].y << "\t";
        }
        std::cout << "\n";
    }
    try {
        for (int ii=0; ii<NX; ++ii){
            //std::cout << ( (data_H2DF1DI[ii].x/sqrtNX - data_HmanyFFT[ii].x) < 1e-7  ) << "\n";
            assert( (data_H2DF1DI[ii].x/sqrtNX - data_HmanyFFT[ii].x)  < 1e-7 );
            assert( (data_H2DF1DI[ii].y/sqrtNX - data_HmanyFFT[ii].y)  < 1e-7 );
        }
    } catch (const char* msg) {
        std::cerr << msg << std::endl;
    }

    //Overwrite GPU data to original values
    ERR_CHECK( cudaMemcpy(data_D, data_H0, sizeof(cufftDoubleComplex) * NX, cudaMemcpyHostToDevice));

    // ******************************************************************************** //
    // ******************************************************************************** //
    // Free stuff
    // ******************************************************************************** //

    cufftDestroy(planMany);cufftDestroy(plan1D);cufftDestroy(plan2D);
    cudaFree(data_D);
    free(data_HmanyFFT);free(data_H0);
    free(data_H2DF1DI);free(data_H1DFFT);
}

void fftIt3D(){
    int dimLength = 5;
    int NX = dimLength*dimLength*dimLength;

    int cbrtNX = std::cbrt(NX);
    int numTransform = cbrtNX*cbrtNX;

    int paramsMatrix[3][5] = {{cbrtNX*cbrtNX,1,1,cbrtNX,0},{cbrtNX,cbrtNX,cbrtNX,1,cbrtNX*cbrtNX},{cbrtNX*cbrtNX,1,cbrtNX*cbrtNX,1,0}};
    FTParams params[3];

    for(int ii=0; ii<3; ++ii){
        params[ii].numTranforms = paramsMatrix[ii][0];
        params[ii].numLoops = paramsMatrix[ii][1];
        params[ii].stride = paramsMatrix[ii][2];
        params[ii].dist = paramsMatrix[ii][3];
        params[ii].offset = paramsMatrix[ii][4];
    }

    int dims[] = {NX};
    int dims3D[] = {cbrtNX,cbrtNX,cbrtNX};

    int inembed[] = {cbrtNX,cbrtNX,cbrtNX};
    int onembed[] = {cbrtNX,cbrtNX,cbrtNX};
    int istride[] = {1,cbrtNX,cbrtNX*cbrtNX}; // Indexed value is respective dimensionality of the transform along a specific dimension.
    int ostride[] = {1,cbrtNX,cbrtNX*cbrtNX};
    int idist[] = {cbrtNX,1,1}; // [Here][] // The next dimension
    int odist[] = {cbrtNX,1,1};

    cufftHandle planMany, plan1D, plan3D;
    cufftDoubleComplex *data_H1DFFT, *data_HmanyFFT, *data_H0, *data_D;

    ERR_CHECK( cudaMalloc( (cufftDoubleComplex**) &data_D, sizeof(cufftDoubleComplex)*NX) );

    data_H1DFFT = (cufftDoubleComplex*) malloc(sizeof(cufftDoubleComplex)*NX);
    data_HmanyFFT = (cufftDoubleComplex*) malloc(sizeof(cufftDoubleComplex)*NX);
    data_H0 = (cufftDoubleComplex*) malloc(sizeof(cufftDoubleComplex)*NX);

    // ******************************************************************************** //
    // Create the input data
    // ******************************************************************************** //
    std::cout << "INPUT:\n";
    for(int ii=0; ii<cbrtNX; ++ii){
		std::cout << "C(:,:," << ii+1 << ")=[";
        for(int jj=0; jj<cbrtNX; ++jj){
            for(int kk=0; kk<cbrtNX; ++kk){
                data_H0[kk + cbrtNX*(jj + ii*cbrtNX)].x = (double) ii;
                data_H0[kk + cbrtNX*(jj + ii*cbrtNX)].y = (double) jj;//(double) jj;
                std::cout << data_H0[kk + cbrtNX*(jj + ii*cbrtNX)].x << " + 1i*" << data_H0[kk + cbrtNX*(jj + ii*cbrtNX)].y << "\t";
            }
            std::cout << "\n";
        }
        std::cout << "]\n";
    }
    std::cout << "\n --- \n";

    ERR_CHECK( cudaMemcpy(data_D, data_H0, sizeof(cufftDoubleComplex) * NX, cudaMemcpyHostToDevice));

    // ******************************************************************************** //
    // First, check the 1D FFT along the standard dimension
    // ******************************************************************************** //
    FFT_ERR_CHECK(cufftPlan1d(&plan1D, cbrtNX, CUFFT_Z2Z, cbrtNX*cbrtNX));
    FFT_ERR_CHECK(cufftExecZ2Z(plan1D, data_D, data_D, CUFFT_FORWARD));
    ERR_CHECK(cudaMemcpy(data_H1DFFT, data_D, sizeof(cufftDoubleComplex) * NX, cudaMemcpyDeviceToHost));
    std::cout << "OUTPUT 1D_1:\n";
    for(int ii=0; ii<cbrtNX; ++ii){
        for(int jj=0; jj<cbrtNX; ++jj){
            for(int kk=0; kk<cbrtNX; ++kk){
                std::cout << data_H1DFFT[kk + cbrtNX*(jj + ii*cbrtNX)].x << " + 1i*" << data_H1DFFT[kk + cbrtNX*(jj + ii*cbrtNX)].y << "\t";
            }
            std::cout << "\n";
        }
        std::cout << "\n";
    }
    std::cout << "\n --- \n";

    //Overwrite GPU data to original values
    ERR_CHECK( cudaMemcpy(data_D, data_H0, sizeof(cufftDoubleComplex) * NX, cudaMemcpyHostToDevice));

    // ******************************************************************************** //
    // ******************************************************************************** //
    // Next, check the Many FFT along the same expected dimension
    // ******************************************************************************** //
    int tDim = 0; //Transform dimension

    int dims2D[] = {cbrtNX,cbrtNX};
    FFT_ERR_CHECK(cufftPlanMany(&planMany, 1, dims2D, inembed, cbrtNX, 1, onembed, cbrtNX, 1, CUFFT_Z2Z, cbrtNX));
    for (int ii=0; ii<cbrtNX; ++ii){
        FFT_ERR_CHECK(cufftExecZ2Z(planMany, &data_D[ii*cbrtNX*cbrtNX], &data_D[ii*cbrtNX*cbrtNX] , CUFFT_FORWARD));
    }

    ERR_CHECK(cudaMemcpy(data_HmanyFFT, data_D, sizeof(cufftDoubleComplex) * NX, cudaMemcpyDeviceToHost));

    std::cout << "OUTPUT MANY 1D:\n";
    for(int ii=0; ii<cbrtNX; ++ii){
        for(int jj=0; jj<cbrtNX; ++jj){
            for(int kk=0; kk<cbrtNX; ++kk){
                std::cout << data_HmanyFFT[kk + cbrtNX*(jj + ii*cbrtNX)].x << " + 1i*" << data_HmanyFFT[kk + cbrtNX*(jj + ii*cbrtNX)].y << "\t";
            }
            std::cout << "\n";
        }
        std::cout << "\n";
    }
    std::cout << "\n --- \n";

    //Overwrite GPU data to original values
    ERR_CHECK( cudaMemcpy(data_D, data_H0, sizeof(cufftDoubleComplex) * NX, cudaMemcpyHostToDevice));

    // ******************************************************************************** //
    // ******************************************************************************** //
    // Free stuff
    // ******************************************************************************** //

    cufftDestroy(planMany);cufftDestroy(plan1D);cufftDestroy(plan3D);
    cudaFree(data_D);
    free(data_HmanyFFT);free(data_H1DFFT);free(data_H0);
}

int main(void) {
    fftMulti3D();
    ERR_CHECK(cudaDeviceReset());
    return (0);
}

Compiling the above code using nvcc ./multiDFFT.cu -o mdfft -lcufft will showcase this method. By performing the FFT in this manner we can achieve approximately 25% improvement over the original 2DF-1DI method. Given that we can make use of the CuFFT internal operations for in-place transforms also allows us to enable memory usage to examine much larger systems sizes without hitting the memory limit (or run the 3D code on smaller consumer GPUs).